1 Intro : rappels divers

1.1 Théorie

le khi2, la régression, et la variance
démarche générale

Avec le khi2, on a vu surtout le test et sa significativité.

Avec la régression, on a abordé uniquement le coefficient de corrélation sans montrer le test.

Avec la variance, nous allons aborder test, significativité et intensité.

1.2 Outils

xls ou csv
libre office ou R

2 Donnée et objet de l’exercice

La variance est utilisée en géographie pour tester des groupements spatiaux.

2.1 Hypothèse

Nous allons étudier la relation entre une variable quantitative et une donnée géographique.

R va nous permettre de mettre en place la donnée d’exemple.

2.2 Préparer la donnée

2.2.1 Que faut-il faire ?

Choisir au moins deux entités administratives, pour nous, le 93 et le 92 et observer si l’épargne nette est équivalente.

Il s’agit de l’épargne disponible pour financer l’investissement des collectivités.

2.2.2 Remarques sur R

opérateur d’assignation
les accolades pour l’indexation
le $ pour la variable
la complétion avec tabulation

Parcours du script et exercice moodle pour voir si c’est compris.

2.2.3 Le script

# lecture du fichier. Quelle remarque faire ?
data <-  read.csv2("data/variance.csv", fileEncoding = "UTF-8", dec =".")
# on ne conserve que le montant par habitant
names (data)

##  [1] "Exercice"                             
##  [2] "Outre.mer"                            
##  [3] "Code.Insee.2024.Région"               
##  [4] "Nom.2024.Région"                      
##  [5] "Code.Insee.2024.Département"          
##  [6] "Nom.2024.Département"                 
##  [7] "Code.Siren.2024.EPCI"                 
##  [8] "Nom.2024.EPCI"                        
##  [9] "Strate.population.2024"               
## [10] "Commune.rurale"                       
## [11] "Commune.de.montagne"                  
## [12] "Commune.touristique"                  
## [13] "Tranche.revenu.par.habitant"          
## [14] "Présence.QPV"                         
## [15] "Code.Insee.2024.Commune"              
## [16] "Nom.2024.Commune"                     
## [17] "Catégorie"                            
## [18] "Code.Siren.Collectivité"              
## [19] "Code.Insee.Collectivité"              
## [20] "Siret.Budget"                         
## [21] "Libellé.Budget"                       
## [22] "Type.de.budget"                       
## [23] "Nomenclature"                         
## [24] "Agrégat"                              
## [25] "Montant"                              
## [26] "Montant.en.millions"                  
## [27] "Population.totale"                    
## [28] "Montant.en...par.habitant"            
## [29] "Compte.2024.Disponible"               
## [30] "code_type_budget"                     
## [31] "ordre_analyse1_section1"              
## [32] "ordre_analyse1_section2"              
## [33] "ordre_analyse1_section3"              
## [34] "ordre_analyse2_section1"              
## [35] "ordre_analyse2_section2"              
## [36] "ordre_analyse2_section3"              
## [37] "ordre_analyse3_section1"              
## [38] "ordre_analyse3_section2"              
## [39] "ordre_analyse3_section3"              
## [40] "ordre_analyse4_section1"              
## [41] "annee_join"                           
## [42] "Population.totale.du.dernier.exercice"

# colonnes 6 et 22, 16 pour avoir le nom de la commune
sel <- data [, c(6,28,16)]
# liste des dpts
unique(sel$Nom.2024.Département)

## [1] "Hauts-de-Seine"    "Seine-Saint-Denis"

# combien de communes  par dpt ?
table(sel$Nom.2024.Département)

## 
##    Hauts-de-Seine Seine-Saint-Denis 
##                36                40

# répartition des communes par dpt ok, on aura quasiment autant de valeurs pour le 92 et le 93
names (sel) <- c("dpt", "montant", "commune")
# on renomme les variables plus simplement

3 Représentation graphique

La boite à moustaches permet de comparer rapidement des distributions. Les moustaches montrent les 1ers et 9e déciles. Les limites des boites correspondent au 1e et 3e quartile Le trait indique la médiane. Les valeurs aberrantes sont les points isolés.

boxplot(sel$montant~sel$dpt )

# Un peu de couleur et des titres
boxplot(sel$montant~sel$dpt, xlab ="Département", ylab="montant épargne nette (euros par hbt)",
        col=rainbow(2))
# Affichage des moyennes sur les boites à moustache
moyenne <- tapply(sel$montant, sel$dpt, mean)
points(moyenne, pch = 2,  col="black", cex = 2)

Ce graphique permet de comparer 2 départements. Les variations entre les groupes sont-elles plus importantes que les variations au sein des groupes eux-mêmes ? A priori, dans le 92, l’amplitude est plus étendue. Les distributions sont très symétriques (la médiane semble au centre de la boite). Il y a autant de communes avec une épargne nette basse qu’avec une épargne dette élevée.

Il existe une très forte valeur négative pour chacun des 2 départements.

sel [sel$montant < 0,]

##                  dpt     montant               commune
## 1     Hauts-de-Seine   -9.255591                Antony
## 7     Hauts-de-Seine  -96.019408      Châtenay-Malabry
## 8     Hauts-de-Seine  -68.760843             Châtillon
## 19    Hauts-de-Seine  -41.607404      Levallois-Perret
## 26    Hauts-de-Seine -654.082223   Le Plessis-Robinson
## 29    Hauts-de-Seine  -47.983874           Saint-Cloud
## 30    Hauts-de-Seine -187.247043                Sceaux
## 35    Hauts-de-Seine  -47.189691         Ville-d'Avray
## 36    Hauts-de-Seine  -49.330382 Villeneuve-la-Garenne
## 38 Seine-Saint-Denis  -32.902027      Aulnay-sous-Bois
## 43 Seine-Saint-Denis -168.095386            Le Bourget
## 69 Seine-Saint-Denis  -43.027696  Saint-Ouen-sur-Seine
## 71 Seine-Saint-Denis  -35.108860                Stains

Les deux communes sont Le Plessis-Robinson pour le 92 et Le Bourget pour le 93

En fait, pour les Hauts de Seine, cette valeur décentre un peu la moyenne.

Mis à part l’amplitude, les deux départements se ressemblent.

4 La variance

4.1 Rappel

Pour mémoire, la variance est le carré de la moyenne des écarts à la moyenne.

Dans le tableur, nous aurions fait une série de tableaux de calcul autour des écarts à la moyennes (en mettant des carrés). Dans R, c’est une formule var.

4.2 Calcul de la variance avec et sans la formule

Pour les 2 dpts

var(sel$montant)

## [1] 19742.05

# Pour l'ensemble de la zone, sans formule
mean((sel$montant - mean(sel$montant))^2)

## [1] 19482.28

Le résultat est légèrement différent, car le logiciel pondère la variance en soustrayant 1 à l’effectif. Plus la série est grande, moins cela a d’importance.

Pour chaque dpt

# on utilise un tapply
tapply(sel$montant, sel$dpt,var)

##    Hauts-de-Seine Seine-Saint-Denis 
##         32194.767          8874.249

La variance est quatre fois plus importante dans le 92 que dans le 93.

5 Analyse de la variance

Attention à bien distinguer la variance de la variation.

La première est la moyenne du carré des écarts, la seconde est juste la somme du carré des écarts.

La variation est une quantité qui se décompose en :

les variations à l’intérieur de chaque groupe (variation intra groupe)
les variations entre les groupes (variation inter groupe)

La variation totale est la somme des deux. La significativité et l’intensité sont calculées avec ces trois grandeurs.

significativité = rapport inter / intra

intensité = rapport inter / total

5.0.1 La formule ANOVA dans R

ANalyse Ordinaire de la VAriance

Sous R, il suffit de lancer une formule.

# transformation en variable de catégorie (une précaution)
sel$dpt <- as.factor(sel$dpt)
modele <- lm (montant ~ dpt, data = sel)
anova(modele)

## Analysis of Variance Table
## 
## Response: montant
##           Df  Sum Sq Mean Sq F value Pr(>F)
## dpt        1    7741    7741  0.3889 0.5348
## Residuals 74 1472913   19904

test <- anova(modele)

Sum Sq = la somme des carrés des écarts (SCE)

Mean Sq = la moyenne des carrés des écarts, c’est la variance sauf qu’au lieu de faire une moyenne classique, on utilise les degrés de liberté pour le dénominateur.

Pour la variation intergroupe, il s’agit du nombre de groupes (dans notre cas, 92 et 93 -1)

Pour la variation intragroupe, l’effectif - le nombre de groupe.

# le nombre de lignes pour les 2 dpts - le nb de dpt
length(sel$dpt) - length(unique(sel$dpt))

## [1] 74

La première ligne (dpt) c’est pour la variation inter-groupe

La deuxième (Residuals) c’est pour l’intérieur des groupes (l’intra)

Que dire ce ces chiffres ?

Comme pour le khi2, on peut faire un test et calculer l’intensité.

5.0.2 Significativité

F value = Test de Fisher, c’est le test de significativité pour l’analyse de la variance.

Le test est mesuré par le rapport entre la variation intergroupe et la variation intragroupe (avec les degrés de liberté).

Si ce rapport est élevé, cela signifie que la variation intergroupe est importante relativement à la variation intra, donc qu’il y a une vraie différence entre les écarts à la moyenne des groupes.

# variation inter / variation intra.
test$`Mean Sq` [1] / test$`Mean Sq` [2]

## [1] 0.3889143

test$`F value`

## [1] 0.3889143        NA

Plus la variation intra augmente, plus le rapport diminue, moins il y a de différence entre les groupes.

5.0.2.1 La table de fisher

Comme pour le khi2, on compare à un test obtenu par le hasard (donc une table).

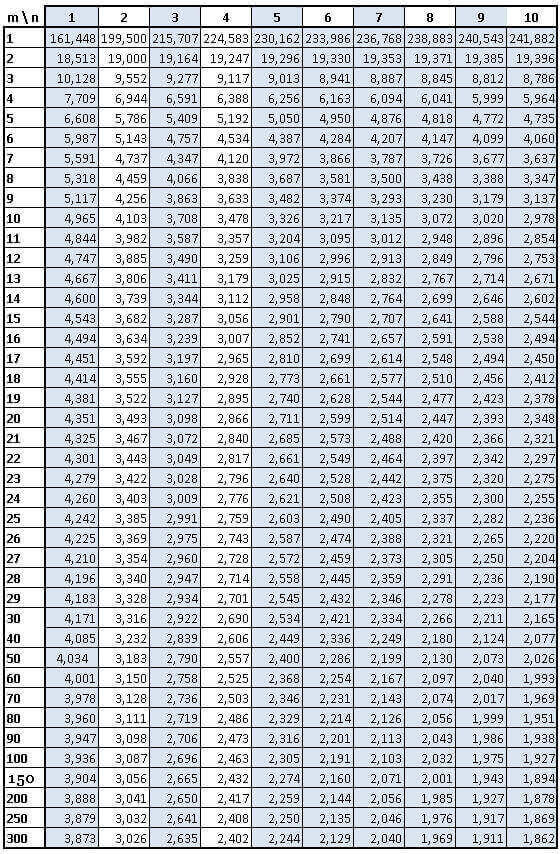F calculé

Ftable <- qf(p=.05, df1=1, df2=74, lower.tail=FALSE)
Fcalcule <- test$`Mean Sq` [1] / test$`Mean Sq` [2]
Ftable

## [1] 3.97023

Fcalcule

## [1] 0.3889143

Le F théorique est supérieur au F calculé pour un risque de 5 %

Il y a indépendance entre les départements et la distribution du montant de l’épargne nette.

5.0.2.2 Avec R, importance de la p-value

Le chiffre le plus rapide à analyser, c’est la p-value, il indique la taille de la différence entre les moyennes des 2 départements

Plus il est petit, plus il y a de différence, plus il est gros, plus les écarts aux moyennes se ressemblent et donc l’hypothèse d’indépendance peut être rejetée.

C’est la même logique que pour le khi2 (cf exemple khi2 dans l’introduction aux bivariées).

Dans notre cas, la pvalue indique un risque important. Concrètement, il faudrait aller chercher la table du risque à % de Fisher.

qf(p=.5348, df1=1, df2=74, lower.tail=FALSE)

## [1] 0.3888919

On a plus de 50 % de chance de se tromper si on rejette l’indépendance, il ne faut donc pas la rejeter.

93 92 ont une même répartition de la dette

5.0.3 Intensité

On mesure également l’intensité, la proportion de la variation expliquée par les modalités dans la variation totale (entre 0 et 1)

variation intergroupe / variation totale

test$`Mean Sq` [1] / sum(test$`Mean Sq`)

## [1] 0.2800132

L’intensité est faible, un plus d’un quart de la variation est expliquée par la structure spatiale.

6 Exercices d’application

6.1 Du département à la région

Le choix est fait de comparer les variations de chaque région.

6.1.1 Hypothèse

Il s’agit d’observer s’il y a une variation entre les régions sur l’ensemble du pays au niveau de l’épargne.

L’hypothèse nulle, comme d’habitude, est qu’il n’y en a pas.

6.1.2 Script

data <- read.csv2("data/varianceSubention.csv", dec = ".")
sel <- data [,c(4,28)]
head(sel)

##        Nom.2024.Région Montant.en...par.habitant
## 1      Hauts-de-France                  40.96386
## 2      Hauts-de-France                 123.17000
## 3 Auvergne-Rhône-Alpes                  60.50586
## 4            Grand Est                 101.28546
## 5            Grand Est                 145.32277
## 6            Grand Est                  51.57234

names(sel) <- c("region", "montant")
(tab <- table(sel$region))

## 
##       Auvergne-Rhône-Alpes    Bourgogne-Franche-Comté 
##                       4024                       3697 
##                   Bretagne        Centre-Val de Loire 
##                       1205                       1755 
##                      Corse                  Grand Est 
##                        360                       5115 
##                 Guadeloupe                     Guyane 
##                         32                         22 
##            Hauts-de-France              Île-de-France 
##                       3776                       1267 
##                 La Réunion                 Martinique 
##                         24                         34 
##                    Mayotte                  Normandie 
##                         17                       2649 
##         Nouvelle-Aquitaine                  Occitanie 
##                       4302                       4453 
##           Pays de la Loire Provence-Alpes-Côte d'Azur 
##                       1231                        945

# Que remarque t on au niveau du nombre de dpts par région ?
(region <- names(tab) [tab > 2000])

## [1] "Auvergne-Rhône-Alpes"    "Bourgogne-Franche-Comté"
## [3] "Grand Est"               "Hauts-de-France"        
## [5] "Normandie"               "Nouvelle-Aquitaine"     
## [7] "Occitanie"

sel2 <- sel [sel$region %in% region,]
table(sel2$region)

## 
##    Auvergne-Rhône-Alpes Bourgogne-Franche-Comté               Grand Est 
##                    4024                    3697                    5115 
##         Hauts-de-France               Normandie      Nouvelle-Aquitaine 
##                    3776                    2649                    4302 
##               Occitanie 
##                    4453

png("img/varianceRegion.png", width = 6000, height = 2000, res = 600)
boxplot(sel$montant~sel$region, las =2)
dev.off()

## png 
##   2

png("img/varianceRegion2.png", width = 6000, height = 2000, res = 600)
boxplot(sel2$montant~sel2$region, las =2)
dev.off()

## png 
##   2

summary(sel2$montant)

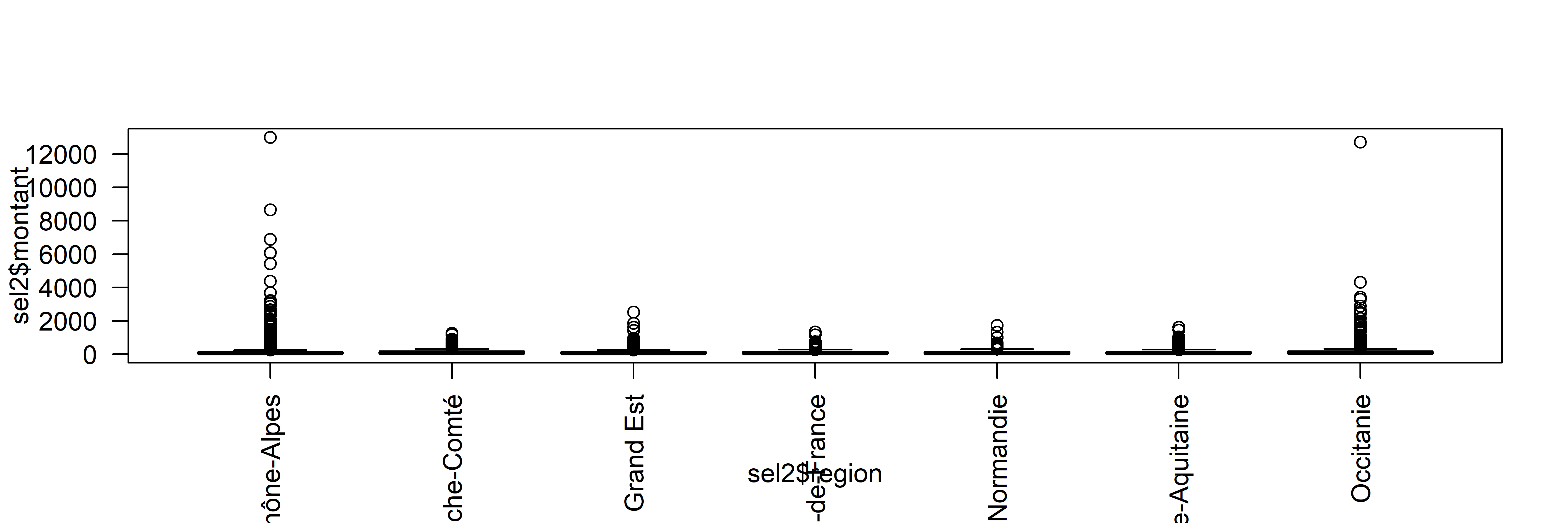
##     Min.  1st Qu.   Median     Mean  3rd Qu.     Max.     NA's 
##     0.00    36.66    72.27   104.22   135.23 13004.32        6

sel3 <- sel2 [sel2$montant < 200 & sel2$montant > - 200,]
png("img/varianceRegion3.png", width = 6000, height = 2000, res = 600)
boxplot(sel3$montant~sel3$region, las=2, xlab = "")
dev.off()

## png 
##   2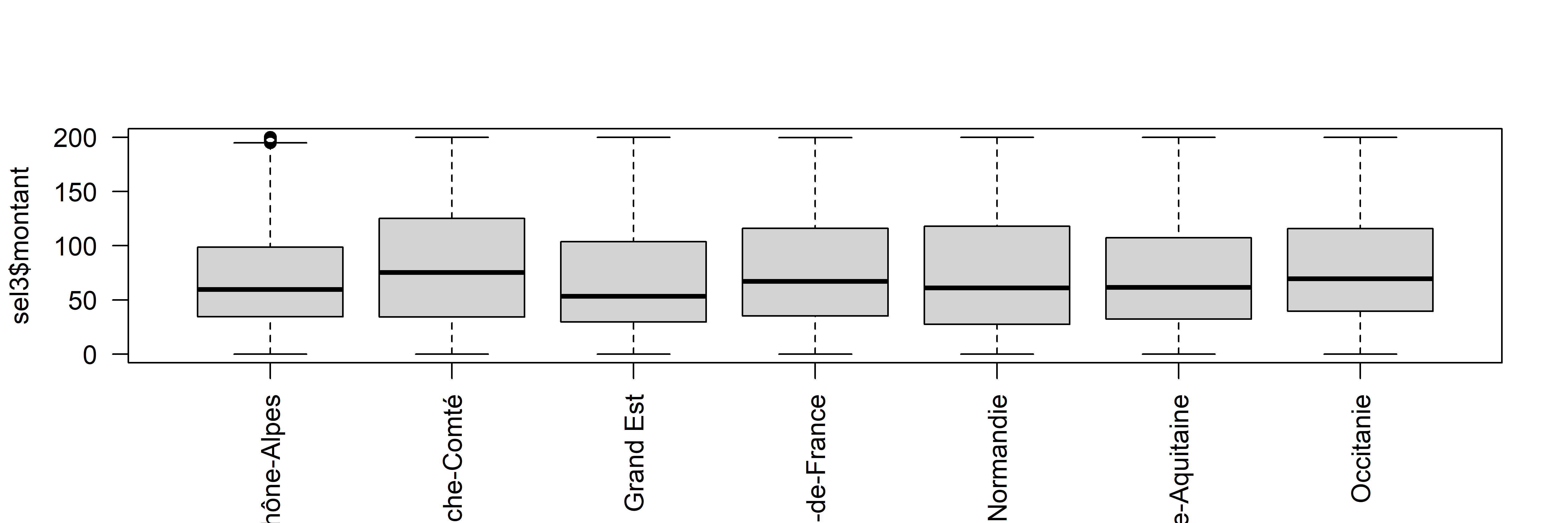

modele <- lm (montant ~ region, data = sel2)
anova(modele)

## Analysis of Variance Table
## 
## Response: montant
##              Df     Sum Sq Mean Sq F value    Pr(>F)    
## region        6    6927580 1154597  30.661 < 2.2e-16 ***
## Residuals 28003 1054498739   37657                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# Intensité
test <- anova(modele)
test$`Mean Sq` [1] / sum(test$`Mean Sq`)

## [1] 0.9684156

L’échelon régional permet d’expliquer 96% de la variation de la dette, mais pas celui de département. (Mais on a conservé uniquement les valeurs entre -200 et 200)

6.2 Correction (année 2022)

6.2.1 Boite à moustaches

Il existe des différences entre les groupes, la variation des notes au sein de chaque groupe est différente. Seul le 3e groupe a une distribution symétrique.

Le premier groupe a des notes de faible amplitudes mais avec 3 notes très fortes. Et le 2e groupe a beaucoup de notes basses.

La variation entre les groupes risque donc d’être plus importante que la variation intragroupe.

6.2.2 Pvalue

Le chiffre de la p-value (0.039) est bas. Donc la relation est significative. H0 est rejetée avec un risque de 4 %.

6.2.2.1 Intensité

L’intensité est forte, plus de 75 % de la variation est expliquée par la structure en groupe.

L5GEABIM Analyses bivariées et multivariées