Statistiques bi variées - base
1 Méthode
1.1 5 étapes
- Hypothèse
- Le tableau de données
- La significativité de la relation : existe-t-elle ?
- L’intensité
- Les écarts au modèle
- Explication géographique
1.2 3 combinaisons
1.2.1 deux types de variables
- continu (quantitatif)
- classe ou catégorie (qualitatif)
Comprendre la différence entre l’histogramme et le graphique à barres, c’est distinguer entre les deux types de variables.
data <- read.csv2("data/fraisPersonnel.csv", fileEncoding = "UTF-8", dec = ".")
par(mfrow = c(2,1))
par(mar = c(4,4,2,2))
hist(data$montant.par.hbt, main = "fréquence absolue", xlab = "classes", ylab="effectif" , border = NA)
par(mar = c(8,4,2,2))
barplot(data$montant.par.hbt, names.arg= data$Nom,main = "distribution", xlab = "", ylab = "frais personnel (€ / hbt", las=2, cex.names = 0.6, border = NA)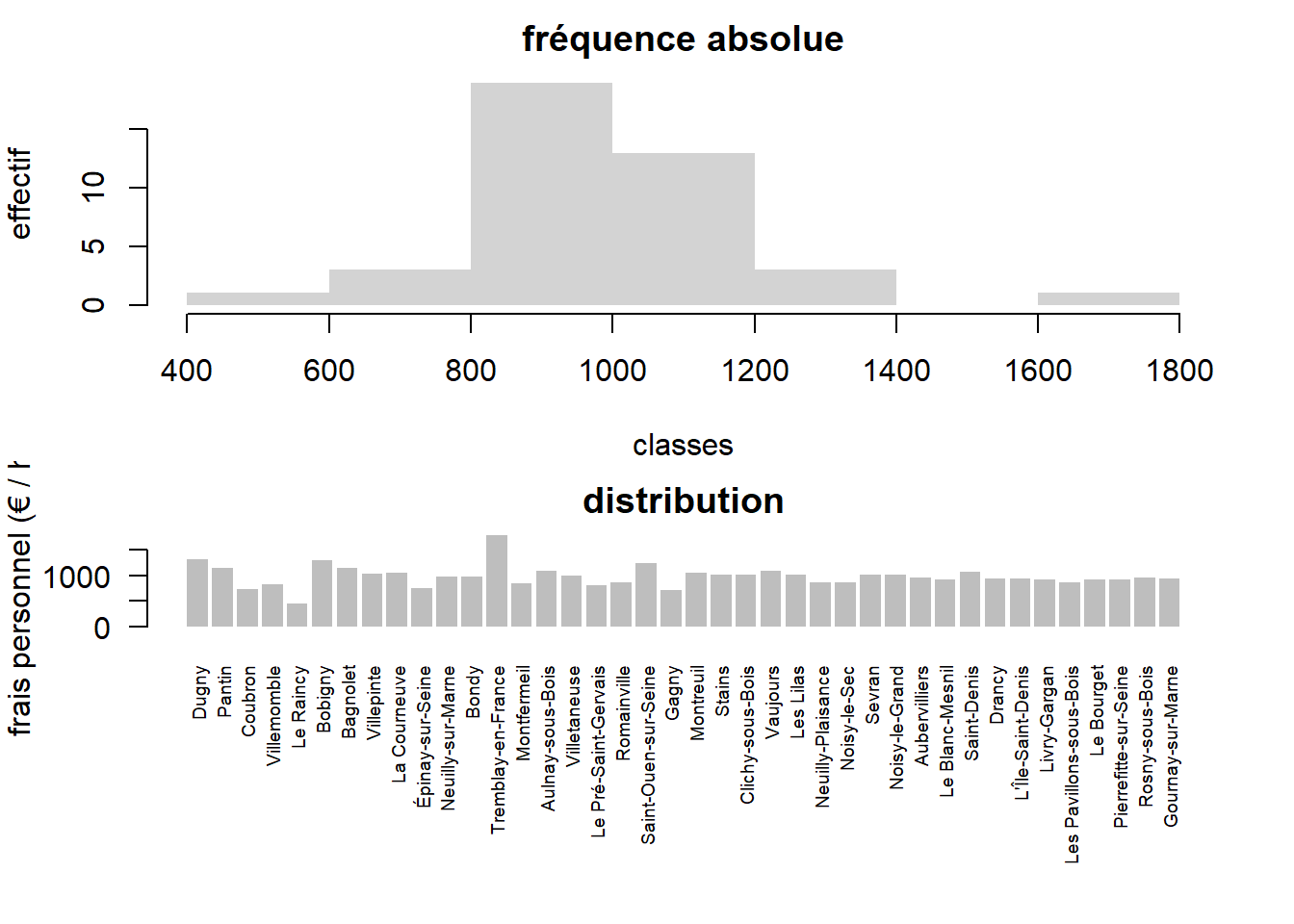
1.2.2 Trois méthodes
Classe / catégorie -> Khi2
Continu -> Régression Correlation
Continu et classe / catégorie -> Analyse de variance
2 Application : prendre 2 variables, donner l’hypothèse et la méthode
Pour chaque exemple, justifier le traitement qu’il faudra utiliser et l’hypothèse de départ qu’il faudra mettre en doute.
2.1 exemple de l’exemple
hypothèse : groupe d’étudiants et réussite à l’examen (oui / non).
hypothèse : nombre de questions en cours et notes à l’examen
hypothèse : groupe d’éudiants et notes finales
2.2 En guise d’introduction pour le khi 2
## Warning in read.table("data/exKHI2.csv", sep = ",", row.names = 1, col.names =
## c("oui", : l'entête et 'col.names' sont de longueurs différentes| oui | non | |
|---|---|---|
| groupe1 | 15 | 15 |
| groupe2 | 27 | 3 |
| groupe3 | 5 | 25 |
##
## Pearson's Chi-squared test
##
## data: data
## X-squared = 32.42, df = 2, p-value = 9.124e-08Il existe un lien entre groupe et résultat, puisque p-value est toute petite.
Certes… mais comment ?
L5GEABIM Analyses bivariées et multivariées